- P203's solution
TJ For 创世纪
- @ 2025-9-6 23:26:36
Subtask #1
考虑每次暴力查询,枚举子区间,对每个子区间进行判断。同时暴力修改即可。
时间复杂度:,空间复杂度:。
Subtask #2
对每个子区间进行判断,时间复杂度过高。考虑直接把全部的子区间的答案存下来,然后修改时暴力修改序列,同时借助序列的信息,修改每个子区间的答案。
时间复杂度:,空间复杂度:。
Subtask #3
考虑优化询问过程,在遍历查询区间时维护当前最长上升、下降序列,上一个最长上升、下降序列的长度,可以线性地解决一次询问。
时间复杂度:,空间复杂度:。
Subtask #4
由于题目给的很好的性质,使人想到可以双指针跑一遍记录所有答案。但这样是离线的,为了支持更改,考虑线段树维护区间操作,区改单查即可。
具体而言,统计双指针区间的答案可以沿用 Subtask #3 的方法,但由于会收缩区间,所以用两个 deque 维护区间中一段段上升和下降序列的长度来方便统计答案。修改操作时用先把双指针区间拓展到修改区间,再用线段树修改,然后根据操作类型更改区间答案:「重塑」时需要把答案改为 ,同时要把 deque 清空;「风蚀」乘负数时需要把交换两个答案,同时要交换两个 deque。询问操作时同样把双指针区间拓展到当前区间,直接输出即可。
时间复杂度:,空间复杂度:。
Subtask #5
看到这个数据范围,没人不想打分块吧。
考虑合并两个整块的答案
(准备好大量分讨和超多变量吧)。
先考虑左边块的最右端高度大于右边块最左端高度时的答案。
令 分别表示红、橙、黄、淡蓝、深蓝线段的长度 (不含黑点)。
一般情况:
- 如下图,这时两个块合并会增加 个「峰」,会增加 个「谷」。
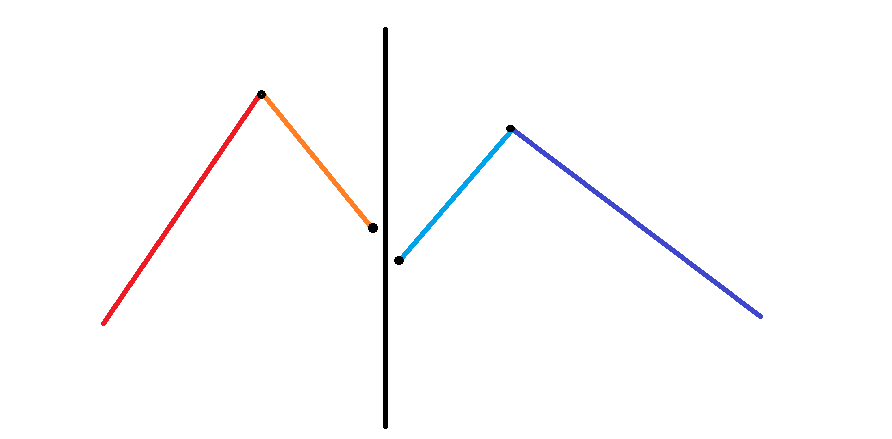
- 如下图,这时两个块合并会增加 个「峰」,会增加 个「谷」。
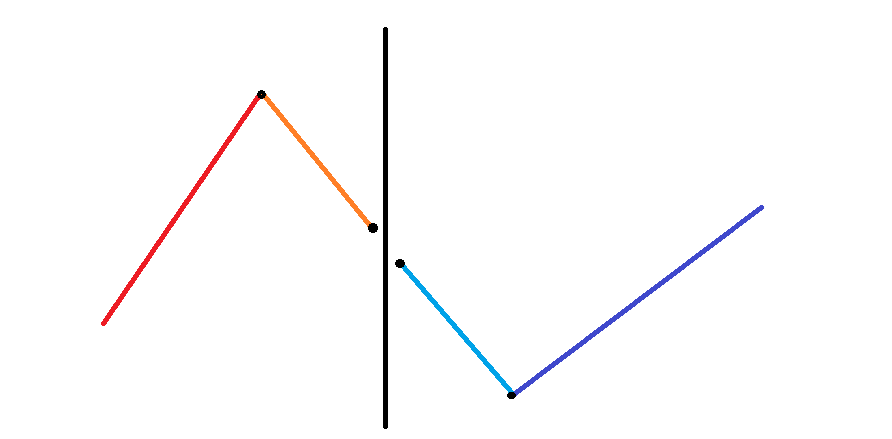
- 如下图,这时两个块合并会增加 个「峰」,会增加 个「谷」。
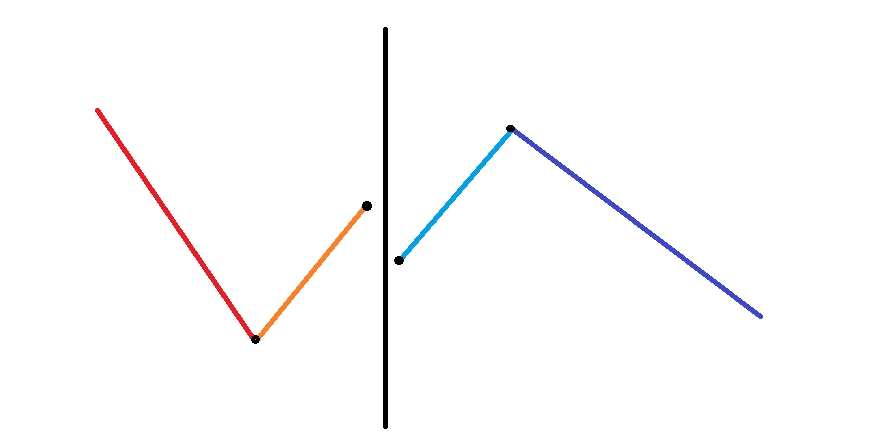
- 如下图,这时两个块合并会增加 个「峰」,会增加 个「谷」。
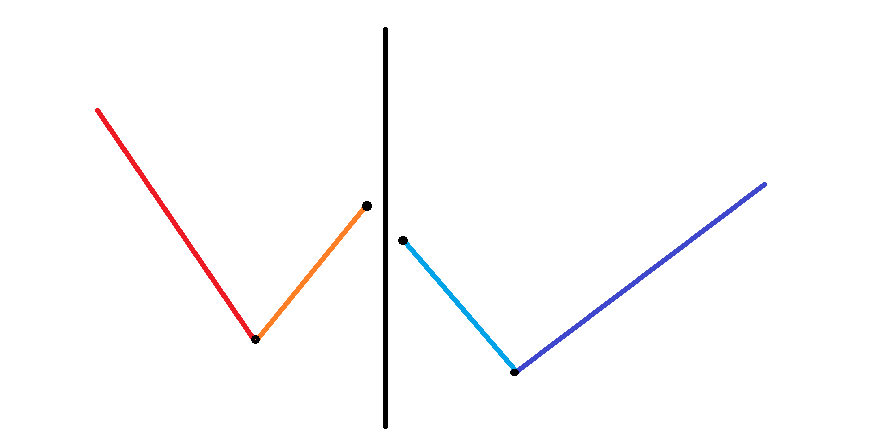
某块的合并处是平的
- 如下图,这时两个块合并会增加 个「谷」。
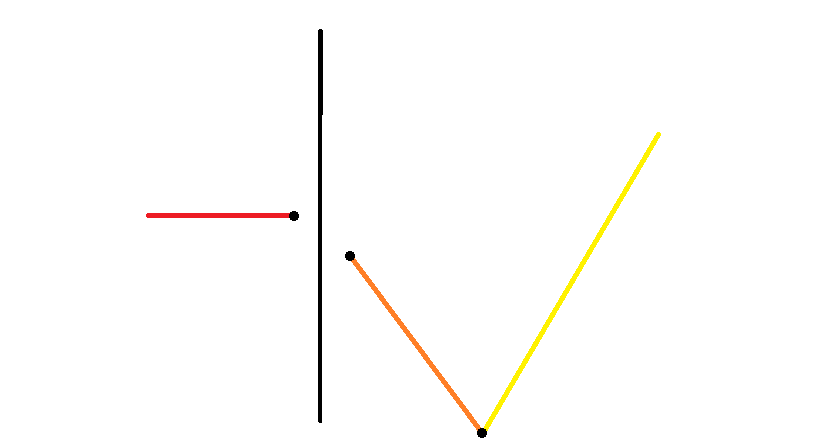
- 如下图,这时两个块合并会增加 个「谷」。
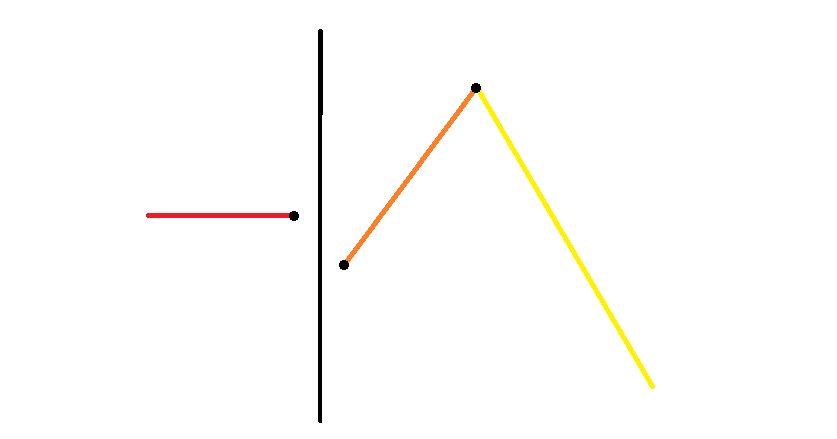
- 如下图,这时两个块合并会增加 个「峰」。
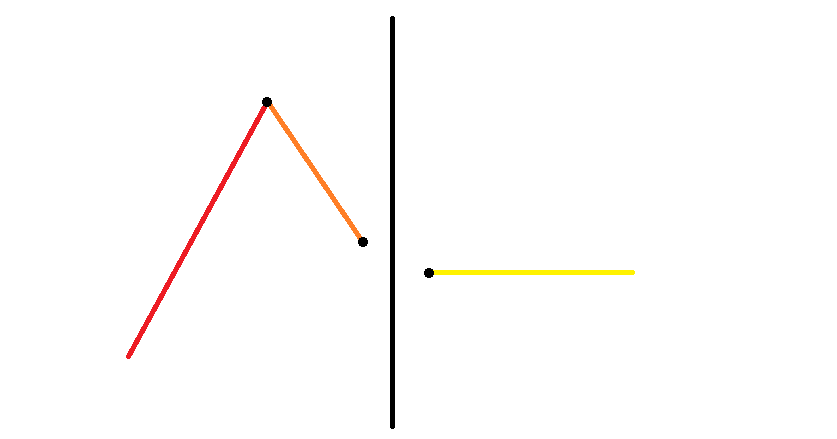
- 如下图,这时两个块合并会增加 个「峰」。
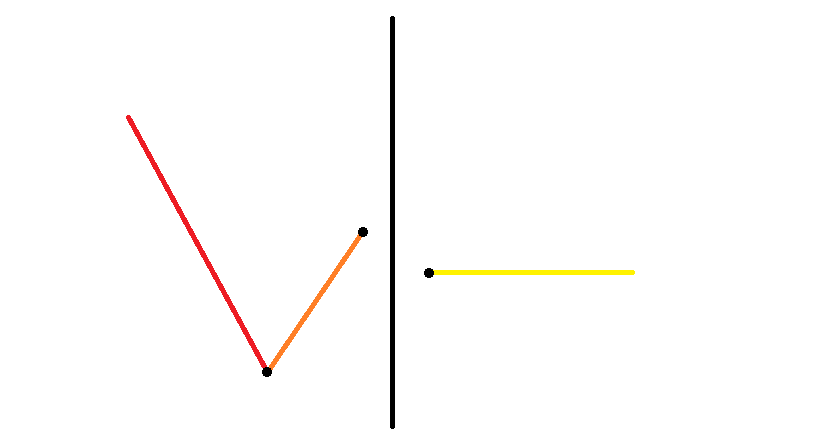
然后考虑左边块的最右端高度小于右边块最左端高度时的答案。
此时的情况和之前大差不差,就不具体赘述了。
考虑合并散块的答案
容易发现可以用 Subtask #3 方法暴力推,然后再把推出来的结果与整块的结果合并一下就行了。
考虑维护的辅助信息
通过上述分析,可以得出我们应该对每个块维护以下信息:
- 和 :记录块中的「峰」、「谷」数量。
- 和 :记录块中以最左边开头的上升、下降序列长度。
- 和 :记录块中以最右边结尾的上升、下降序列长度。
- :记录以最左边开头的下降序列结束后的上升序列长度。
- :记录以最左边开头的上升序列结束后的下降序列长度。
- :记录以最右边结尾的下降序列开始前的上升序列长度。
- :记录以最右边结尾的上升序列开始前的下降序列长度。
- 和 :记录块最左端、最右端的高度。
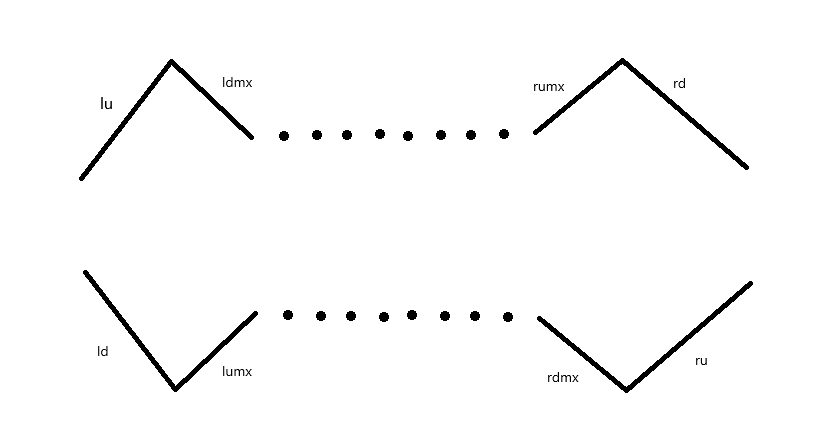
然后考虑我们应该怎样在合并时更新它们:
对于 和 前面已经提到过,而 和 、 和 更新比较简单,所以重点放在 、、、。
接下来以 的更新为例:
同样令 分别表示红、橙、黄线段的长度 (不含黑点)。
- 如下图, 应该加上 。
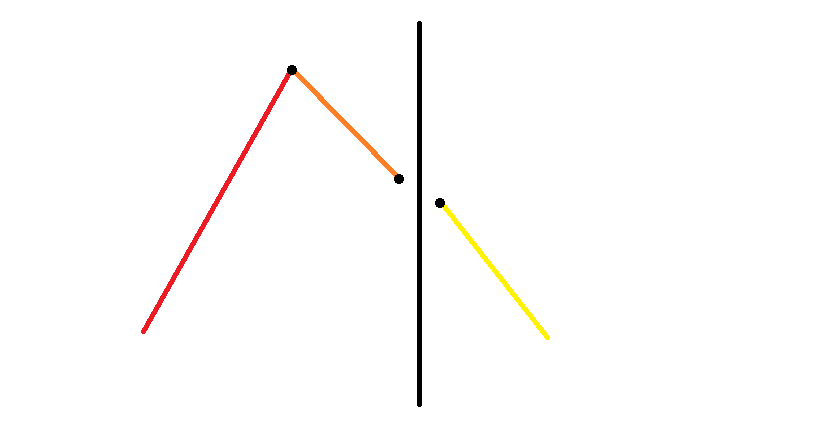
- 如下图, 应该加上 。
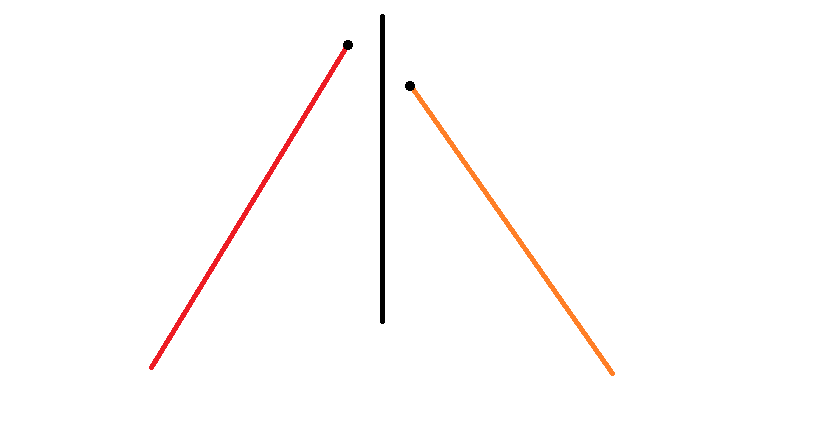
- 如下图, 应该加上 。
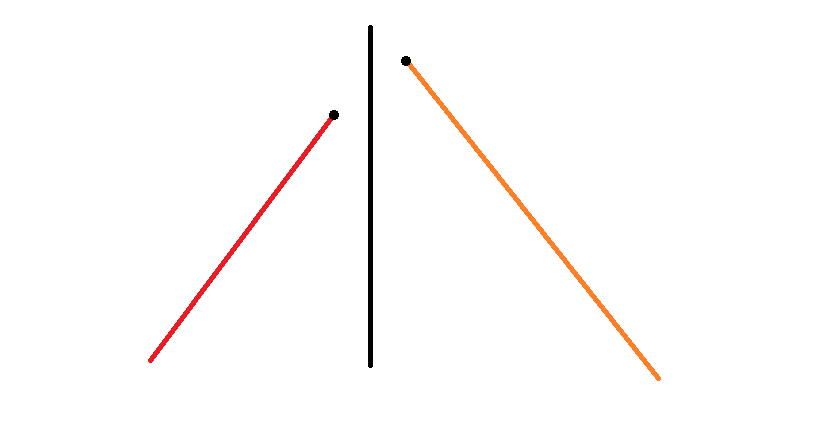
- 如下图, 应该加上 。
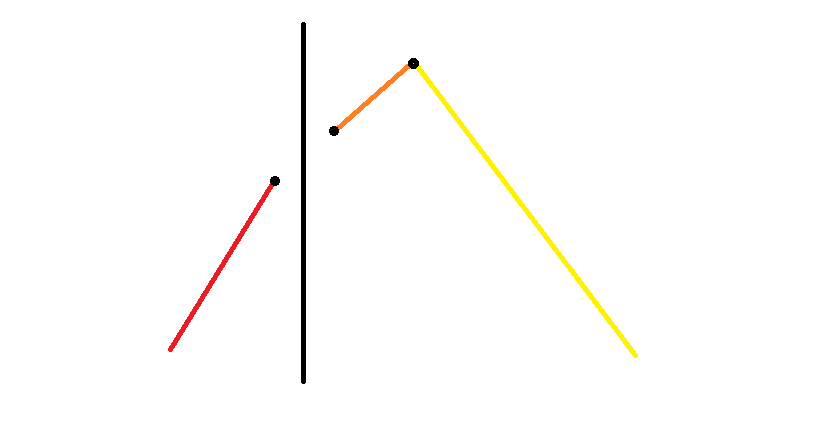
至于剩下的,不过多赘述。
考虑操作对信息的影响
由于只有加法,稍微想想就知道对大多数信息没影响,只 、 加上 即可。
总之细节繁多,码量巨大,常数一坨,特殊性质也跟有似的,但确实减少了一定码量。
时间复杂度:,空间复杂度:。
Subtask #6
发现之前维护的东西具有区间可加性,可以换做线段树维护,虽然常数照样巨大。
没了特殊性质 B,我们要考虑一下负数和其他操作的情况。
考虑操作对信息的影响
「造陆」:
显然对大多数信息没影响,同样只需要 、 加上 即可。
「风蚀」:
由于题目的保证,也对大多数信息没影响,只需要 、 乘上 即可。
乘一个负数可以看作把区间大小颠倒之后再乘一个正数,区间颠倒只需要把对应的数值交换即可。
「重塑」:
显然操作后需要把很多信息置零,再把 、 改为 即可。
懒标记操作的顺序应该是 ,这样最好写,同时不要忘了操作对懒标记的影响。
时间复杂度:,空间复杂度:。
代码
#include<bits/stdc++.h>
#define double long double
//不用long double也行
using namespace std;
const int N=5e5+1,inf=1e18;
const double zps=1e-5,fps=-1e-5;//精度控制
struct node{
int cntf,cntg,len,ld,lu,ldmx,lumx,rd,ru,rdmx,rumx;
double lt,rt,mn,mx,add,mul,cov;
node(){cntf=cntg=len=ld=lu=ldmx=lumx=rd=ru=rdmx=rumx=lt=rt=add=0,mul=1,mn=cov=inf,mx=-inf;}
}s[N<<2],res;
#define mid ((l+r)>>1)
#define ls k<<1
#define rs k<<1|1
inline void merge(node&k,node&x,node&y){//冗长的merge
k.len=x.len+y.len;
k.ld=x.ld==x.len&&x.rt-y.lt>zps?x.len+y.ld:x.ld;
k.lu=x.lu==x.len&&x.rt-y.lt<fps?x.len+y.lu:x.lu;
k.rd=y.rd==y.len&&x.rt-y.lt>zps?y.len+x.rd:y.rd;
k.ru=y.ru==y.len&&x.rt-y.lt<fps?y.len+x.ru:y.ru;
//对ldmx,lumx,rdmx,rumx的更新
k.ldmx=x.ldmx,k.lumx=x.lumx,k.rdmx=y.rdmx,k.rumx=y.rumx;
if(x.lu+x.ldmx==x.len&&x.len+y.len>2&&abs(x.rt-y.lt)>zps){
if(x.lu==x.len){
if(x.rt-y.lt<fps)k.ldmx=max(y.ld-1,y.ldmx);
else if(x.len>1)k.ldmx=y.ld;
}else if(x.rt-y.lt>zps&&x.ldmx)k.ldmx=x.ldmx+y.ld;
}
if(x.ld+x.lumx==x.len&&x.len+y.len>2&&abs(x.rt-y.lt)>zps){
if(x.ld==x.len){
if(x.rt-y.lt>zps)k.lumx=max(y.lu-1,y.lumx);
else if(x.len>1)k.lumx=y.lu;
}else if(x.rt-y.lt<fps&&x.lumx)k.lumx=x.lumx+y.lu;
}
if(y.ru+y.rdmx==y.len&&x.len+y.len>2&&abs(x.rt-y.lt)>zps){
if(y.ru==y.len){
if(x.rt-y.lt<fps)k.rdmx=max(x.rd-1,x.rdmx);
else if(y.len>1)k.rdmx=x.rd;
}else if(x.rt-y.lt>zps&&y.rdmx)k.rdmx=y.rdmx+x.rd;
}
if(y.rd+y.rumx==y.len&&x.len+y.len>2&&abs(x.rt-y.lt)>zps){
if(y.rd==y.len){
if(x.rt-y.lt>zps)k.rumx=max(x.ru-1,x.rumx);
else if(y.len>1)k.rumx=x.ru;
}else if(x.rt-y.lt<fps&&y.rumx)k.rumx=y.rumx+x.ru;
}
k.lt=x.lt,k.rt=y.rt,k.mn=min(x.mn,y.mn),k.mx=max(x.mx,y.mx);
//对cntf,cntg的更新
k.cntf=x.cntf+y.cntf,k.cntg=x.cntg+y.cntg;
if(abs(x.rt-y.lt)<=zps)return;
if(x.rt-y.lt>zps){
if(x.rd>1&&y.ld>1)k.cntf+=x.rumx*y.ld,k.cntg+=x.rd*y.lumx;
if(x.rd>1&&y.lu>1)k.cntf+=x.rumx,k.cntg+=x.rd*(y.lu-1);
if(x.ru>1&&y.ld>1)k.cntf+=(x.ru-1)*y.ld,k.cntg+=y.lumx;
if(x.ru>1&&y.lu>1)k.cntf+=x.ru-1,k.cntg+=y.lu-1;
if(x.rd>1&&x.rumx&&y.lu==1&&y.ld==1)k.cntf+=x.rumx;
if(x.ru>1&&y.lu==1&&y.ld==1)k.cntf+=x.ru-1;
if(x.ru==1&&x.rd==1&&y.lumx&&y.ld>1)k.cntg+=y.lumx;
if(x.ru==1&&x.rd==1&&y.lu>1)k.cntg+=y.lu-1;
}
if(x.rt-y.lt<fps){
if(x.rd>1&&y.ld>1)k.cntf+=y.ld-1,k.cntg+=x.rd-1;
if(x.rd>1&&y.lu>1)k.cntf+=y.ldmx,k.cntg+=(x.rd-1)*y.lu;
if(x.ru>1&&y.ld>1)k.cntf+=x.ru*(y.ld-1),k.cntg+=x.rdmx;
if(x.ru>1&&y.lu>1)k.cntf+=x.ru*y.ldmx,k.cntg+=x.rdmx*y.lu;
if(x.rd>1&&y.lu==1&&y.ld==1)k.cntg+=x.rd-1;
if(x.ru>1&&x.rdmx&&y.lu==1&&y.ld==1)k.cntg+=x.rdmx;
if(x.ru==1&&x.rd==1&&y.ld>1)k.cntf+=y.ld-1;
if(x.ru==1&&x.rd==1&&y.ldmx&&y.lu>1)k.cntf+=y.ldmx;
}
}
//以下就是普通线段树
inline void newnode(int k){
cin>>s[k].lt,s[k].rt=s[k].mn=s[k].mx=s[k].lt;
s[k].len=s[k].ld=s[k].lu=s[k].rd=s[k].ru=1;
}
inline void addnode(int k,double v){
s[k].lt+=v,s[k].rt+=v,s[k].mx+=v,s[k].mn+=v,s[k].add+=v;
}
inline void covnode(int k,double v){
s[k].lt=s[k].rt=s[k].cov=s[k].mx=s[k].mn=v;
s[k].cntf=s[k].cntg=s[k].ldmx=s[k].lumx=s[k].rdmx=s[k].rumx=s[k].add=0;
s[k].ld=s[k].lu=s[k].rd=s[k].ru=s[k].mul=1;
}
inline void mulnode(int k,double v){
if(v==0)return covnode(k,0);//乘0就直接覆盖成0
s[k].lt*=v,s[k].rt*=v,s[k].mn*=v,s[k].mx*=v,s[k].mul*=v,s[k].add*=v;
if(v<0)swap(s[k].ld,s[k].lu),swap(s[k].rd,s[k].ru),swap(s[k].ldmx,s[k].lumx),swap(s[k].rdmx,s[k].rumx),swap(s[k].cntf,s[k].cntg),swap(s[k].mn,s[k].mx);
}
inline void pushup(int k,int l,int r){
merge(s[k],s[ls],s[rs]);
}
inline void pushdown(int k){//注意先后顺序
if(s[k].cov!=inf)covnode(ls,s[k].cov),covnode(rs,s[k].cov),s[k].cov=inf;
if(s[k].mul!=1)mulnode(ls,s[k].mul),mulnode(rs,s[k].mul),s[k].mul=1;
if(s[k].add)addnode(ls,s[k].add),addnode(rs,s[k].add),s[k].add=0;
}
void build(int k,int l,int r){
if(l==r)return newnode(k);
build(ls,l,mid),build(rs,mid+1,r);
pushup(k,l,r);
}
void add(int k,int l,int r,int x,int y,double v){
if(x<=l&&r<=y)return addnode(k,v);
pushdown(k);
if(x<=mid)add(ls,l,mid,x,y,v);
if(y>mid)add(rs,mid+1,r,x,y,v);
pushup(k,l,r);
}
void mul(int k,int l,int r,int x,int y,double v){
if(x<=l&&r<=y)return mulnode(k,v);
pushdown(k);
if(x<=mid)mul(ls,l,mid,x,y,v);
if(y>mid)mul(rs,mid+1,r,x,y,v);
pushup(k,l,r);
}
void cov(int k,int l,int r,int x,int y,double v){
if(x<=l&&r<=y)return covnode(k,v);
pushdown(k);
if(x<=mid)cov(ls,l,mid,x,y,v);
if(y>mid)cov(rs,mid+1,r,x,y,v);
pushup(k,l,r);
}
double askmn(int k,int l,int r,int x,int y){
if(x<=l&&r<=y)return s[k].mn;
double res=inf;pushdown(k);
if(x<=mid)res=min(res,askmn(ls,l,mid,x,y));
if(y>mid)res=min(res,askmn(rs,mid+1,r,x,y));
return res;
}//要判断操作会不会使区间的结果大于1e9或小于-1e9
double askmx(int k,int l,int r,int x,int y){
if(x<=l&&r<=y)return s[k].mx;
double res=-inf;pushdown(k);
if(x<=mid)res=max(res,askmx(ls,l,mid,x,y));
if(y>mid)res=max(res,askmx(rs,mid+1,r,x,y));
return res;
}
node ask(int k,int l,int r,int x,int y){
if(x<=l&&r<=y)return s[k];
node lres,rres,res;
pushdown(k);
if(x<=mid)lres=ask(ls,l,mid,x,y);
if(y>mid)rres=ask(rs,mid+1,r,x,y);
if(!rres.len)return lres;
if(!lres.len)return rres;
return merge(res,lres,rres),res;
}
double v;
int op,l,r,n,m;
inline bool chk(double x){//精度判断
return (double)(-1e9+fps)<=x&&x<=(double)(1e9+zps);
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m,build(1,1,n);
while(m--){
cin>>op>>l>>r;
switch(op){
case 0:res=ask(1,1,n,l,r),cout<<res.cntf<<' '<<res.cntg<<'\n';break;
case 1:cin>>v,chk(askmx(1,1,n,l,r)+v)&&chk(askmn(1,1,n,l,r)+v)?add(1,1,n,l,r,v):void();break;
case 2:cin>>v,chk(askmx(1,1,n,l,r)*v)&&chk(askmn(1,1,n,l,r)*v)?mul(1,1,n,l,r,v):void();break;
case 3:cin>>v,cov(1,1,n,l,r,v);break;
}
}
return 0;
}
