题目描述

给定 $N$ 个感叹号（即一条线段和一个点），求一个最小的圆（即半径最小），使得每个感叹号都与圆周或圆的内部有至少一个交点（线段或点与圆周或圆的内部有至少一个交点）。

输入格式

第一行输入 $T$，代表数据组数。

每组数据：

• 第 $1$ 行是 $N$。
• 第 $2\sim N+1$ 行：每行 $6$ 个整数 $X_{i_1},Y_{i_1},X_{i_2},Y_{i_2},X_{i_3},Y_{i_3}$，表示第 $i$ 个感叹号中线段的端点坐标为 $(X_{i_1},Y_{i_1})$ 和 $(X_{i_2},Y_{i_2})$、点的坐标为 $(X_{i_3},Y_{i_3})$。

输出格式

对于每组数据，一行输出 $3$ 个整数 $A,B,R$，分别表示圆的顶点坐标为 $(A,B)$，半径为 $R$。

样例 #1

样例输入 #1

1
5
1 2 3 4 5 6
7 8 9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30

样例输出 #1

15.000000 16.000000 14.142136

提示

样例 $\bm{\#1}$ 解释

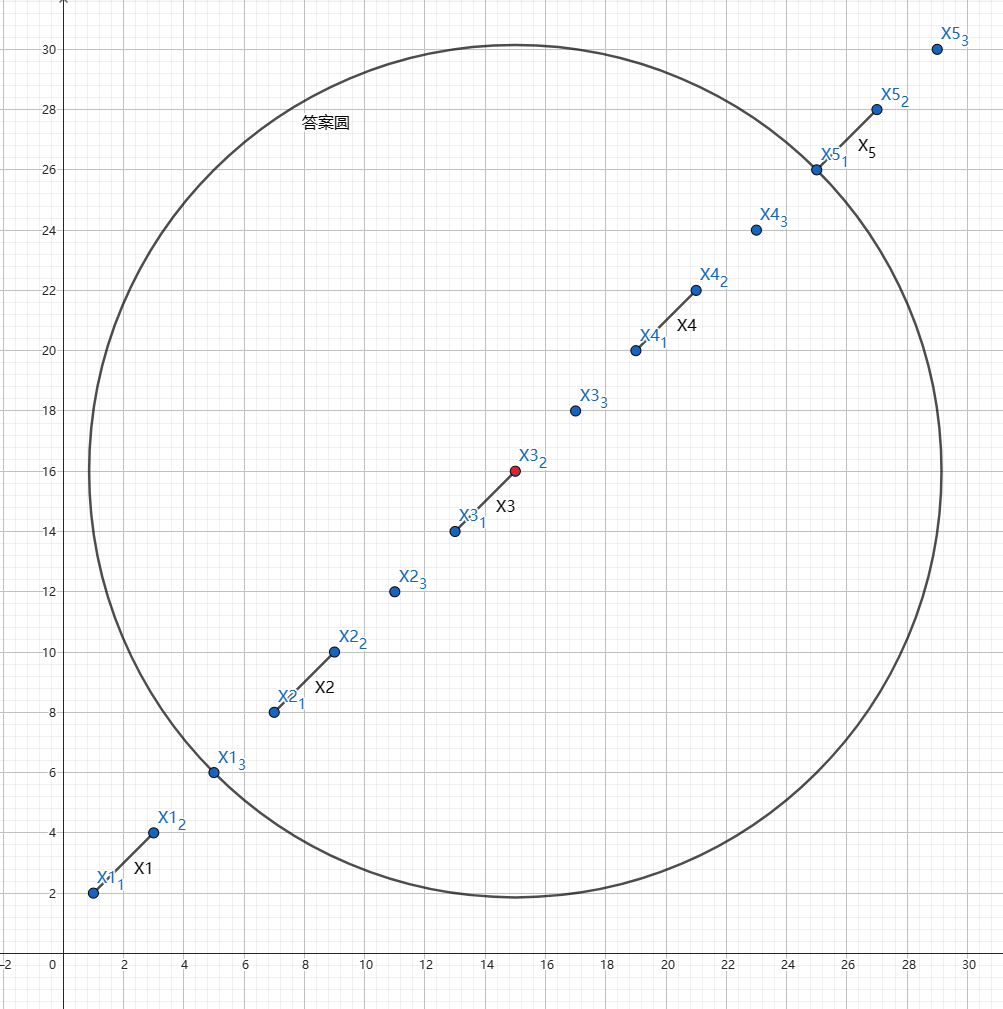
最小圆如图，红点为圆心。

• 本题开启 $\textsf{\textbf{\colorbox{orange}{\color{white}{Special Judge}}}}$，任何相对误差不超过 $10^{-2}$ 的正确答案都会被判对；特别地，在数据中，$T=1$ 或 $5$，每个测试点的 $10$ 分将被平均分给 $T$ 组测试数据。
• 对于每组数据输出的 $3$ 个数，全部正确则得到该组数据的全部分数；若有 $2$ 个数是正确的，你将得到该组数据的 $50\%$ 的分数；否则你将无法得到该组数据的分数。
• 本题不捆绑测试点。
• $0\leq X_{i_1},Y_{i_1},X_{i_2},Y_{i_2},X_{i_3},Y_{i_3}\leq 10^4$；

$^{\color{red}{*}}$：此测试点保证 $0\leq X_{i_1},Y_{i_1},X_{i_2},Y_{i_2},X_{i_3},Y_{i_3}\leq 10^2$。