该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

注意

本题不需要使用文件读写。

在你输出一行后，请使用 fflush(stdout); / cout.flush(); / cout << endl; 清空缓冲区。

你可以尝试使用 unsigned short 存储海拔信息以优化空间常数。

题目背景

Sleeping Bear 是一只十分可爱的小熊，它越吃蜂蜜就越可爱，可是它每次去摘蜂蜜都会被蜜蜂蛰一头包。今天它又要吃蜂蜜了，但是它不想又被蜜蜂蛰一头包，所以它想请你帮助它设计一条逃生路线以躲避蜜蜂的围追堵截。

题目描述

给定一个正整数 $k$，表示有一个 $k \times k$ 的地图，其中每一格都有自己的海拔。海拔是一个 $[0,k^2-1]$ 范围内的正整数。保证海拔为 $0,1,\ldots,k^2-1$ 的格子各有一个。

已知 Sleeping Bear 所在的位置（默认蜜蜂就在它身后），不能走的路，可以走的路以及湖的位置（只有 Sleeping Bear 跳入湖中才能不被蜜蜂蛰）：

• Sleeping Bear 可能在任何一个海拔大于 $x$ 而小于 $y$ 的位置；
• 所有海拔不大于 $x$ 的位置都被水淹没，形成了湖；
• 所有海拔不小于 $y$ 的位置都被雪覆盖，形成了雪山，不能走；
• 所有海拔大于 $x$ 而小于 $y$ 的位置都是可以走的路；
• 保证 $x<y$。

在接下来的 $q$ 天里，Sleeping Bear 每天都要去吃蜂蜜，而每天的天气都不同（这导致每天的 $x,y$ 都不同）。请你帮助 Sleeping Bear 数一数，有多少个海拔大于 $x$ 而小于 $y$ 的位置不存在通往湖边的路（他每次可以向上、下、左、右移动一格）。

输入格式

第一行输入两个整数 $k,q$，表示有一个 $k \times k$ 的地图，而你一共要解决 Sleeping Bear 的 $q$ 个问题。

接下来 $k$ 行，每行输入 $k$ 个非负整数，表示这个地方的海拔。保证海拔为 $0,1,\ldots,k^2-1$ 的格子各有一个。

接下来 $q$ 行，每行输入两个非负整数 $x,y$（保证 $x<y$），表示 Sleeping Bear 的一个问题。

输出格式

对于 Sleeping Bear 的每个问题，输出一行一个非负整数。

Sleeping Bear 要求你在他给出一个问题后立即回答（也就是说，他要求你强制在线）。在你回答他的这个问题之前，你将无法得到下一个问题的输入。

样例

5 4
9 12 21 7 4
22 18 17 13 10
5 23 1 3 19
16 6 20 14 2
0 15 24 11 8
0 15
4 18
11 22
1 14

14
2
0
7

10 10
0 1 2 3 4 5 6 7 8 9 
10 11 12 13 14 15 16 17 18 19 
20 21 22 23 24 25 26 27 28 29 
30 31 32 33 34 35 36 37 38 39 
40 41 42 43 44 45 46 47 48 49 
50 51 52 53 54 55 56 57 58 59 
60 61 62 63 64 65 66 67 68 69 
70 71 72 73 74 75 76 77 78 79 
80 81 82 83 84 85 86 87 88 89 
90 91 92 93 94 95 96 97 98 99 
0 1
1 2
2 3
3 5
5 8
8 13
13 21
21 34
34 55
55 89

0
0
0
0
0
0
0
0
0
0

提示

样例 $1$ 解释：

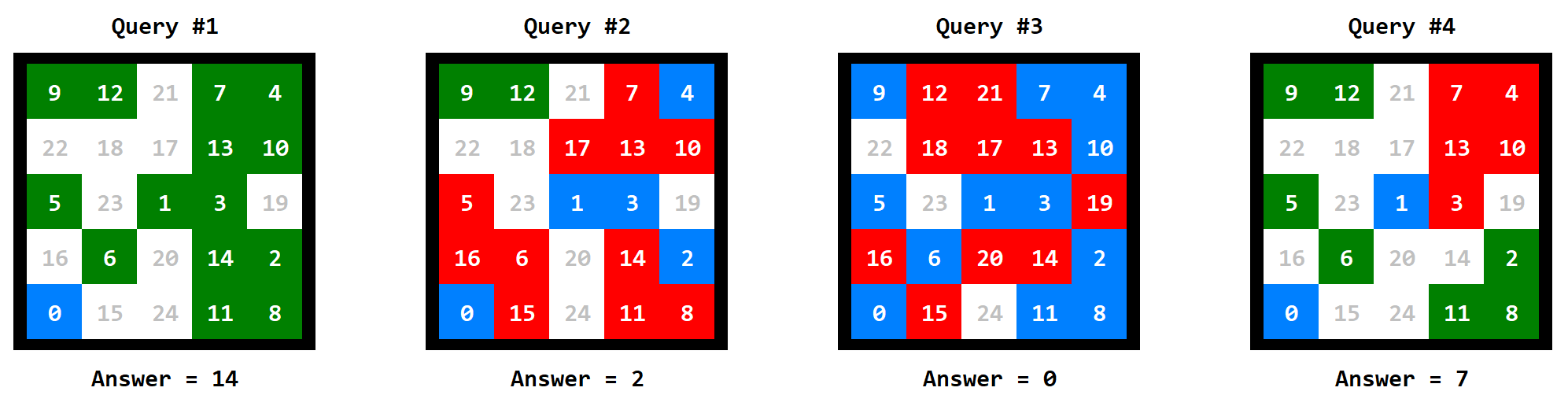
如图，绿色位置不存在通往湖边的路，红色位置存在通往湖边的路，故答案为 $14,2,0,7$。

• 对于 $50\%$ 的数据，$2 \le k \le 10$，$1 \le q \le 100$。
• 对于 $100\%$ 的数据，$2 \le k \le 250$，$1 \le q \le 10^5$。
• 保证地图上海拔为 $0,1,\ldots,k^2-1$ 的格子各有一个。
• 保证 $0\le x<y\le k^2-1$。